As the scale of deep learning models grows, so does the computational and memory cost associated with fine-tuning these models for specific tasks. Fine-tuning a large model can involve adjusting billions of parameters, which is resource-intensive and often impractical. Parameter-efficient fine-tuning (PEFT) techniques have been developed to address this issue, allowing for model adaptation with fewer parameters and without the need to modify or store the entire model. One notable approach to PEFT is Low-Rank Adaptation (LoRA), which offers an innovative way to fine-tune large models efficiently.
Overview of Parameter-Efficient Fine-Tuning
Parameter-efficient fine-tuning focuses on updating a subset of parameters in a model or using additional small, task-specific modules that require fewer parameters to be learned. By reducing the number of parameters that need to be fine-tuned, the computational resources required for training are significantly decreased. Common Techniques
Fine-Tuning Only the Last Layer: This approach freezes all model layers except the last layer, where task-specific parameters are added. For example, a classification head is added to the final layer to map the model’s output embeddings to the desired classes. Although this technique is simple and computationally efficient, it may not be ideal for tasks requiring substantial adaptation, as only the final layer is fine-tuned.
Adapter Layers: Adapter layers involve adding small, task-specific layers between the model’s existing layers. These new layers contain a small number of additional parameters and learn the task-specific transformation needed to adapt the pre-trained model. Adapter layers introduce minimal computational overhead and allow for task-specific customization while retaining most of the original model’s parameters.
Low-Rank Adaptation (LoRA)
LoRA is a parameter-efficient fine-tuning technique that leverages matrix factorization to reduce the number of parameters that need to be adjusted.
The Concept of Rank Decomposition
Matrix Rank:
- Rank of a matrix refers to the minimum number of independent rows or columns within it.
- A low-rank matrix has fewer independent rows/columns than the number of dimensions, meaning it has intrinsic structure that can be compressed.
Low-Rank Adaptation (LoRA):
LoRA proposes that the updates to a model’s weights can often be represented in a low-dimensional subspace. The central idea is to approximate the changes in model weights as the product of two low-rank matrices:
- \(W= W_{0} + ΔW ≈ W_{0}+BA\) where:
- \(W_{0}\) is the original large model weight matrix,
- \(ΔW\) is the fine-tuned weight change,
- B and A are low-rank matrices.
Of course, A and B alone may not capture all the information ΔW would capture, but this is by design. In LoRA, we hypothesize that the model requires W to be a large, full-rank matrix to capture all the knowledge in the pretraining dataset. However, during fine-tuning, we don’t need to update all weights.
Implementation in LoRA
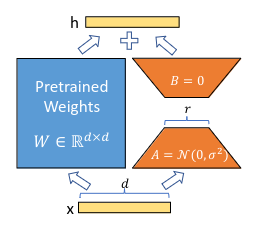
A significant advantage of LoRA is that it allows us to keep the original model weights unchanged by introducing adaptable, low-rank updates separately. By leveraging the distributive property of matrix multiplication, we can express fine-tuning in a simplified way:
In traditional fine-tuning, we update the model weights directly:
\[x \cdot (W + \Delta W) = x \cdot W + x \cdot \Delta W\]
where \(x\) is the input, \(W\) is the original weight matrix, and \(\Delta W\) represents the full set of fine-tuned weight adjustments.
With LoRA, however, we approximate \(\Delta W\) as the product of two low-rank matrices \(A\) and \(B\):
\[x \cdot (W + A \cdot B) = x \cdot W + x \cdot A \cdot B\]
This representation provides two important benefits:
- Preservation of Original Weights: Since the LoRA matrices \(A\) and \(B\) are separate from \(W\), the original model weights remain unchanged. This enables us to add task-specific adaptations without overwriting any of the pretrained model’s knowledge.
- Memory Efficiency: LoRA only requires storing the low-rank matrices \(A\) and \(B\), which dramatically reduces memory overhead. During training or inference, we can apply these matrices dynamically to modify the model’s behavior on-the-fly.
By treating the LoRA updates as additive terms rather than direct modifications to the weights, we achieve parameter-efficient fine-tuning. This is especially beneficial in scenarios where we want to retain the pretrained model’s integrity or handle multiple tasks with the same base model.
Code implementation of LoRA
import torch
import torch.nn as nn
class LoRALayer(nn.Module):
"""
LoRALayer implements a parameter-efficient fine-tuning layer using low-rank adaptation.
"""
def __init__(self, in_dim, out_dim, rank, alpha):
"""
Initializes the LoRALayer with specified dimensions and scaling factor.
in_dim : int
The input dimension of the layer.
out_dim : int
The output dimension of the layer.
rank : int
The rank for the low-rank matrices A and B.
alpha : float
The scaling factor applied to the output of the layer.
"""
super().__init__()
std_dev = 1 / torch.sqrt(torch.tensor(rank).float())
self.A = nn.Parameter(torch.randn(in_dim, rank) * std_dev)
self.B = nn.Parameter(torch.zeros(rank, out_dim))
self.alpha = alpha
def forward(self, x):
"""
Performs the forward pass by applying the low-rank adaptation to the input.
"""
x = self.alpha * torch.matmul(torch.matmul(x, self.A), self.B)
return xThere are two key hyperparameters control the fine-tuning process namely rank and alpha
- The rank hyperparameter determines the inner dimension of the low-rank matrices A and B, effectively controlling the degree of parameter reduction and the representational capacity of the adaptation. A smaller rank means fewer parameters are added, making the adaptation more parameter-efficient
- The second hyperparameter alpha, serves as a scaling factor applied to the output of the low-rank adaptation. This scaling factor influences the extent to which the adaptation modifies the original layer output.
What is the optimal rank to choose might seem like a highly important to ask at first glance. However, as per the authors, it doesn’t matter technically. LoRA performs well with lower ranks and is more than sufficient.
To summarize we have seen what LoRA is all about, how LoRA is implemented, and also the code implementation of it.