The concept of Attention is essential to the working of the Transformer. Through this concept of attention, models focus on the relevant information to give predictions.
Take an example of a sentence
The sky is ___ and world is round.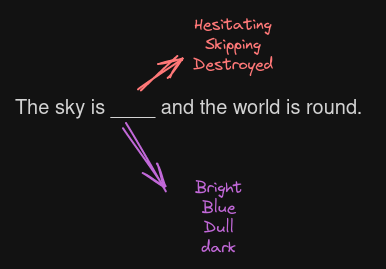
What words might you use to fill in the blanks for the above sentence? Given the context, it is quite evident to see words like “hesitating”, “destroyed”, and “skipping” are unrelated.
Language models need to understand the relationship between the words to predict words that fit into the context and are relevant. This is where the concept of Attention enters, which is central to the functioning of the transformers alongside other concepts and features like the position encoding, tokenizers, and the feed-forward layers.
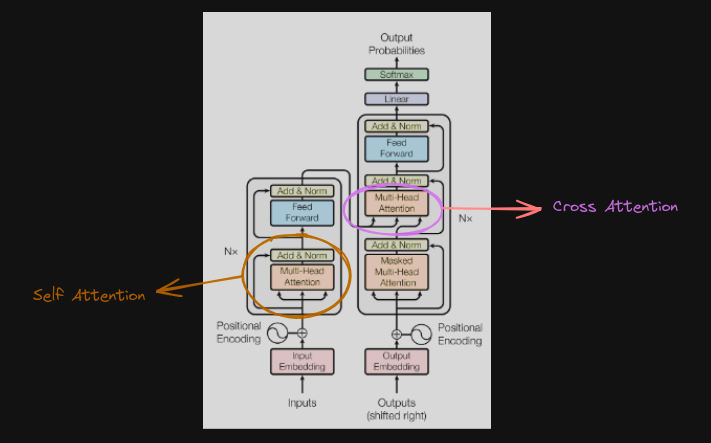
Self Attention
Put it is a sequence-to-sequence operation where a sequence of vectors are manipulated using a set of operations to result in a sequence of vectors, where both the input and the output have the same set of dimensions.
The operation utilizes three matrices namely Query,Key and Value denoted by - \(W_q\) , \(W_k\) , \(W_v\)
The Query , Key, Value pairs are obtained by matrix multiplication between \(W\) and \(x\) where \(W\) is the weight matrices and \(x\) is the embedding inputs
- \(q^{(i)} = W_{(q)} \times x^{i}\)
- \(k^{(i)} = W_{(k)} \times x^i\)
- \(v{(i)} = W_{(v)} \times x^{i}\) where \(i\) \(\epsilon\) \([1,T]\) where T is the length of input sequence and i is index of token
The query and key vectors has same number of elements , elements present in value vector is arbitrary. The operations that take place are sequentially are
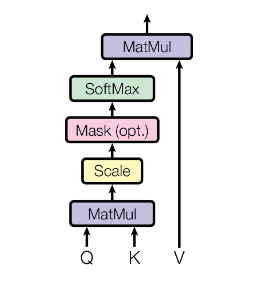
- Matrix multiplication
- Scaling
- Mask (needed in seq to seq translation or autoregressive generation)
- Softmax
- Matrix multiplication
Let us now dive deep into these individual operations
Generating Query,Key,Value matrices
Let us Load the libraries before proceeding
import torch
import mathStart with the random input sequence, which has been pre-processed through an embedding layer. Feel free to modify the input text and experiment. This results in feature vectors \(x_{1},…,x_{n}\), each with a dimension of \(1×d\). Together, these vectors form a matrix \(X\) of size \(n×d\).
text = "The sky is blue and world is round"
ignore_chars = ",';#$@&)("
for char in ignore_chars:
text = text.replace(char,'')
stoi = {s:i for i,s in enumerate(sorted(text.split()))}Convert the input text to token ids
itos = torch.tensor([stoi[s] for s in text.replace(ignore_chars,'').split()],dtype= torch.int64)
itos
### output:
tensor([0, 6, 5, 3, 1, 7, 5, 3])Use the Embedding layer to transform the token ids to their respective feature vectors. The vocabulary size and the dimensions of the model can be changed .
vocab_size = 100 #number of unique vocabulary
d_model = 32 #dimension of feature vectors
embeddings = torch.nn.Embedding(vocab_size,d_model)
X = embeddings(itos)Now that the feature vectors are present we can use them to generate the Query,Key and Value matrices.
W_q = torch.randn(d_model, d_model)
W_k = torch.randn(d_model, d_model)
W_v = torch.randn(d_model, d_model)
Q = X.matmul(W_q)
K = X.matmul(W_k)
V = X.matmul(W_v)The size of all the three matrices will be torch.Size([8, 32]). We will now proceed through the steps to modify the respective matrices 
Matrix Multiplication of Query and Key
This is the first operation performed and building it from the ground up it is a dot product of the vector \(q_{i}\) with the vector \(k_{i}\). With regards to the dot product operation, one of them is a row vector and the other has to be a column vector. Thus we see the key vector to be transposed.

Since this has to be applied on the query and key matrix, a matrix multiplication operation is performed and the resultant output is called compatibility matrix.
compat_matrix = Q.matmul(K.T)Scaling of the compatibility matrix
We know scale the output of the previous step by dividing the matrix by factor of \(\frac{1}{\sqrt{d_{k}}}\) , where \(d_{k}\) is the dimension of the key vector.
Now a question should arise , why do we have to divide it by \(\frac{1}{\sqrt{d_{k}}}\) , what does it do ?
This is done to adjust the range of the dot product and ensure more stable gradients. As the dimensions become large, if it is not scaled, the variance of the keys and values increases. Finally ending up in a phenomenon named vanishing gradients after the softmax operation is performed.Vanishing gradients problem can lead to an unstable training process.
scaled_compat_matrix = 1.0/math.sqrt(d_model) * compat_matrix#understanding the effect of variance
print(f"Variance of compatibility matrix:{torch.var(compat_matrix).item()}")
print(f"Variance of scaled compatibility matrix:{torch.var(scaled_compat_matrix).item()}")
### output
Variance of compatibility matrix:38521.3046875
Variance of scaled compatibility matrix:1203.790771484375We can see a drastic difference in the variance of the matrix, thus we perform the scaling of the compatibility matrix.
Softmax operation on compatibility matrix
The softmax operation is used to yield the matrix of attention weights within the range of 0 to 1. This operation is performed as it can effectively represent the probabilities of the individual values in the input sequence. Also applying it to the entire matrix transforms the output into a probability distribution.
#softmax operation
attention_matrix = torch.softmax(scaled_compat_matrix, dim=0)Matrix multiplication with Value matrix
We know perform matrix multiplication on the matrix obtained from the previous step with the Value matrix to obtain the context matrix. There is no need of transposing of matrices here as the dimensions for both of the matrices involved are the same 
results = attention_matrix.matmul(V)
print(results.shape)
### output
torch.Size([8, 32])Summing it up this is the code for the self-attention process
class SelfAttention(torch.nn.Module):
def __init__(self, embed_size):
super(SelfAttention, self).__init__()
self.embed_size = embed_size
self.query = torch.nn.Linear(embed_size, embed_size)
self.key = torch.nn.Linear(embed_size, embed_size)
self.value = torch.nn.Linear(embed_size, embed_size)
self.scale = torch.sqrt(torch.FloatTensor([embed_size]))
def forward(self, x):
Q = self.query(x)
K = self.key(x)
V = self.value(x)
scores = torch.matmul(Q, K.transpose(-2, -1)) / self.scale
attention = F.softmax(scores, dim=-1)
out = torch.matmul(attention, V)
return outMulti Head Attention
We got to see how self-attention works, and what the point of multi-head attention might be our next question.
Take the analogy of a detective trying to solve a puzzle, while the detective may be smart enough to solve it, it does take a lot of time to investigate and then arrive at conclusions. imagine the advantage the detective might have if there is a team of 3 or 4 people with him. One can investigate in person and the other might help in writing reports etc. The presence of the team helps in accelerating the process. It is the same with regards to multi-head attention as well.
When dealing with sequences consisting of multiple interrelated relationships, self-attention fails to capture it as it has a limited capacity to attend.
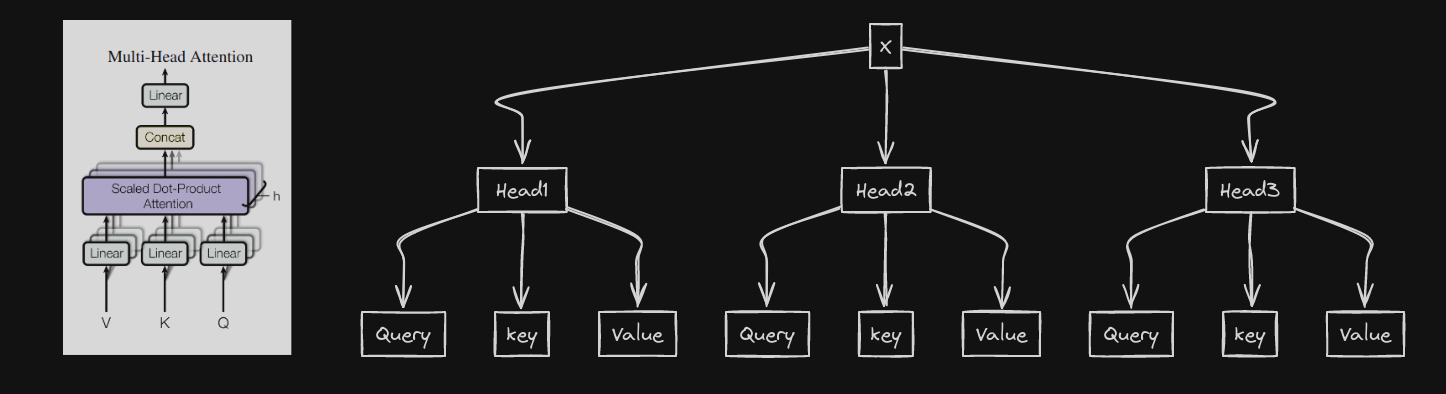
While similar fundamental operations we performed in Self-Attention process takes place here too but with respective to the individual heads present. Once the operations are completed, they are then concatenated in the end.
Computation of attention weights
Given an input sequence(\(X\)):
Project input into queries \(Q_i\), keys \(K_i\), and values \(V_i\) for each head \(i\):
\(Q_i = XW_i^Q, \quad K_i = XW_i^K, \quad V_i = XW_i^V\)
Compute scaled dot-product attention for each head:
\(\text{Attention}(Q_i, K_i, V_i) = \text{softmax}\left(\frac{Q_i K_i^T}{\sqrt{d_k}}\right)V_i\)
Concatenate outputs from all heads:
\(\text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_h)W^o\)
where \(W^o\) is the output projection matrix.
The code to perform this operation
class MultiHeadAttention(nn.Module):
def __init__(self, d_model, num_heads):
super(MultiHeadAttention, self).__init__()
assert d_model % num_heads == 0, "d_model must be divisible by num_heads"
self.d_model = d_model
self.num_heads = num_heads
self.head_dim = d_model // num_heads
self.W_q = nn.Linear(d_model, d_model)
self.W_k = nn.Linear(d_model, d_model)
self.W_v = nn.Linear(d_model, d_model)
self.W_o = nn.Linear(d_model, d_model)
def split_heads(self, x):
batch_size, seq_length, _ = x.size()
return x.view(batch_size, seq_length, self.num_heads, self.head_dim).transpose(1, 2)
def forward(self, query, key, value, mask=None):
batch_size, seq_length, _ = query.size()
Q = self.split_heads(self.W_q(query))
K = self.split_heads(self.W_k(key))
V = self.split_heads(self.W_v(value))
# Scaled dot-product attention
scores = torch.matmul(Q, K.transpose(-2, -1)) / (self.head_dim ** 0.5)
if mask is not None:
scores = scores.masked_fill(mask == 0, float('-inf'))
attention_weights = F.softmax(scores, dim=-1)
attention_output = torch.matmul(attention_weights, V)
# Concatenate heads and apply final linear layer
attention_output = attention_output.transpose(1, 2).contiguous().view(batch_size, seq_length, self.d_model)
output = self.W_o(attention_output)
return output, attention_weightsLet us initialize the number of parameters and the dimension of feature vector.
num_heads = 4 #number of heads
d_model = 32 dimension of feature vectors
mha = MultiHeadAttention(d_model, num_heads)
X_batch = X.unsqueeze(0)
output, attention_weights = mha(X_batch, X_batch, X_batch)
print("Output shape:", output.shape)
print("Attention weights shape:", attention_weights.shape)
### output
Output shape: torch.Size([1, 8, 32])
Attention weights shape: torch.Size([1, 4, 8, 8])In sum, we’ve explored the inner workings of both Self-Attention and Multi-Head Attention, which are foundational to the transformative ‘Transformer’ model. We got to see how the self-attention mechanism works, from matrix multiplication to scaling, and then why softmax is used. As well as understanding why MultiHead Attention is needed and how it can help in better understanding of the complexities present in input text.
References
- Attention is all you need - The OG paper
- Sebastian Raschka elegant explanation of Self Attention
- Modern Approach in NLP Book - Detailed walkthrough of the concepts